GEMM with Shared Memory Tiling
Recap: Naive GEMM Limitations
In our previous exploration of naive GEMM implementation, we discovered that despite achieving optimal memory access patterns—broadcast reads for Matrix A and coalesced reads for Matrix B—performance remained severely limited at approximately 2% of theoretical peak.
The root cause was poor data reuse due to cache capacity constraints. While our (32,32) block configuration created efficient warp-level memory patterns, frequent cache evictions forced repeated global memory accesses for the same data elements. This resulted in a memory-bound kernel unable to fully utilize the GPU’s computational resources.
Moving Forward: Shared Memory as the Solution
To overcome these limitations of naive GEMM, we need explicit control over data locality and reuse. The L1 cache, being a hardware-managed cache controlled by the execution framework, provides no guarantee that data brought into cache will remain available for subsequent transactions.
Shared memory, managed by the programmer and often called a “software cache,” provides a solution by allowing programmers to control data movement explicitly. Once data is loaded into shared memory, it is guaranteed to remain available until either overwritten by the program or the kernel execution completes.
However, it is not possible to bring all matrix data into shared memory simultaneously. To understand why, let us examine the key limitations that prevent this approach:
CUDA Programming Constraints - Ampere Architecture
Understanding memory and thread limitations when developing CUDA applications for matrix operations.
Shared Memory Constraints
Thread Block Limitations
Tiling Strategy Options for 256×256 Matrices
These constraints reveal that while matrix A cannot fit entirely into one thread block’s shared memory, it can be split into smaller sub-matrices (tiles) that do fit. This approach forms the foundation of Tiled GEMM, where matrices are divided into manageable tiles that individual thread blocks can process effectively using shared memory. The tiling strategy is designed from the output matrix’s perspective.
Tiling Strategy Options
Several tiling strategies can be used to partition the 256×256 matrices into smaller sub-matrices. The tile size significantly impacts both memory usage and thread utilization, so it must be chosen carefully to achieve optimal performance. from the below listed we can’t proceed with some of the options due to limitations we discussed earlier like number of threads per block , ex:- 64 64 tile needs 4096 threads per block , but the maximum number of threads per block configuration is 1024, hence we can eliminate the Tile sizes 128128 & 6464, for our example we will consider tile size of 3232.
Calculations
Matrix Size: 256 × 256 = 65,536 elements For tile size T×T: Number of tiles = (256/T)²
• 128×128 tiles: (256/128)² = 2² = 4 tiles • 64×64 tiles: (256/64)² = 4² = 16 tiles • 32×32 tiles: (256/32)² = 8² = 64 tiles • 16×16 tiles: (256/16)² = 16² = 256 tiles • 8×8 tiles: (256/8)² = 32² = 1,024 tiles • 4×4 tiles: (256/4)² = 64² = 4,096 tiles
Tiling Step by Step:
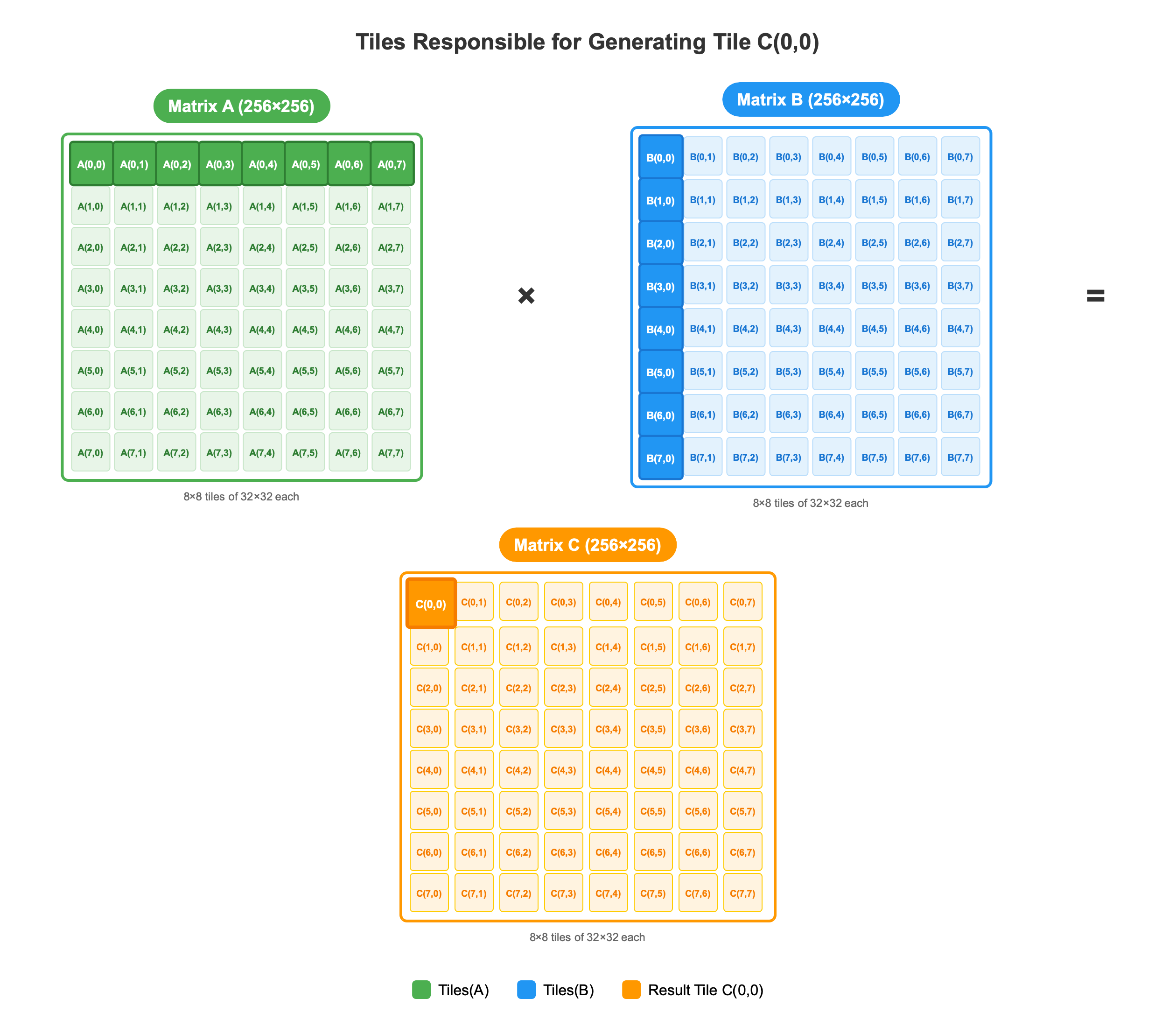
Next Steps: We’ll examine how Thread Block (0,0) processes these tiles through the 8 sequential phases to compute C(0,0) using shared memory optimization.
Full Grid Execution: This visualization represents the computation of a single tile C(0,0). Simultaneously, the remaining 63 thread blocks execute identical processes to compute their assigned tiles, covering the complete 8×8 tile grid from C(0,0) to C(7,7). The collective output of all 64 thread blocks yields the final 256×256 matrix containing 65,536 elements.








Data Reuse Analysis: Naive GEMM vs Tile GEMM
Let us examine how tiling solves the data reuse inefficiencies that arise in naive GEMM cache evictions.
Configuration Recap:
Naive GEMM: Grid of 1,024 thread blocks (32×32 grid), each thread block containing 1,024 threads (32×32), with no shared memory usage.
Tiled GEMM: Grid of 64 thread blocks (8×8 grid), each thread block containing 1,024 threads (32×32), using 32×32 tiles with shared memory for matrices A and B.
If we revisit the configuration and execution for Naive GEMM , our configuration comprised Grid of 64 Thread Blocks in 2D (32,32) & Thread Block comprised of 1024 threads in 2D (32,32) , each Thread block had 8 Warps, each warp calculating 32 elements in output matrix.
Data Reuse Analysis
Naive GEMM Limitations:
To calculate adjacent output elements C(0,0) and C(0,1), both require the entire first row of matrix A. While this row is loaded once from global memory for C(0,0), cache evictions prevent reuse for C(0,1), forcing redundant global memory accesses.
In order to calculate C(0,0) and C(1,0) we need the first column of B matrix i.e B(0,0) => B(0,31), while calculating C(0,0) this whole column had been fetched from Global memory and used for C(0,0) the same could not be reused for performing computations for C(1,0) due to cache evictions, we will briefly look at the steps in Warp-0
Memory Access per Thread Block (Naive):
Load Row-0 from Matrix A: 256 × 4 bytes = 1 KB Load Columns 0-31 from Matrix B: 256 × 32 × 4 bytes = 32 KB
Data Loading from Global Memory:
- Matrix A: 1 row = 256 elements × 4 bytes = 1,024 bytes
- Matrix B: 1 column = 256 elements × 4 bytes = 1,024 bytes
- Total: 2,048 bytes
Operations Performed:
256 multiply operations + 256 add operations = 512 FLOPs
Arithmetic Intensity:
512 FLOPs ÷ 2,048 bytes = 0.25 FLOPS/Byte
Problem: Matrix B columns cannot be reused across computations due to cache evictions
Tiled GEMM Solution:
Data Loading from Global Memory:
- Load 32×32 tile from Matrix A into shared memory: 32 × 32 × 4 bytes * 8 Tiles = 32 KB
- Load 32×32 tile from Matrix B into shared memory: 32 × 32 × 4 bytes * 8 Tiles = 32 KB
- Total: 64 KB = 65,536 bytes
Operations Performed:
32×32 threads × 512 operations each = 524,288 FLOPs
Arithmetic Intensity:
524,288FLOPs ÷ 65,536 bytes = 8.0 FLOPS/Byte
Key Observation: The improvement comes from data reuse within shared memory. In tiled GEMM, each byte loaded from global memory is reused multiple times across different computations, while in naive GEMM, each byte is used only once before being potentially evicted from cache.


Performance Analysis
To understand optimizations achieved by Tiled GEMM, we need to understand the theoritical limits of Hardware to calculate Arthimatic Inensity for both Naive & Tiled GEMM
A100 Specifications
- CUDA Cores: 6,912 (108 SMs × 64 cores per SM)
- Base Clock: ~1.41 GHz
- Memory: 80GB HBM2e
- Memory Interface: 5,120-bit bus width
- Memory Clock: ~1.6 GHz (effective)
Peak FLOPS Calculation
- Cores per SM: 64 CUDA cores
- Total SMs: 108 streaming multiprocessors
- Total CUDA cores: 108 × 64 = 6,912 cores
- Base clock frequency: ~1.41 GHz
- Operations per core per clock: 1 FMA = 2 FLOPs
Peak FP32 Performance:
Peak FLOPS = Total Cores × Clock Frequency × FLOPs per Clock Peak FLOPS = 6,912 × 1.41 × 10⁹ × 2 Peak FLOPS ≈ 19.5 TFLOPS
Peak Memory Bandwidth Calculation
Memory interface width: 5,120 bits = 640 bytes Memory clock (effective): ~1,600 MHz (DDR, so 800 MHz × 2)
Peak Memory Bandwidth:
Peak Bandwidth = Interface Width × Memory Clock Peak Bandwidth = 640 bytes × 1,600 × 10⁶ transfers/second Peak Bandwidth ≈ 2,039 GB/s ≈ 2.0 TB/s
Peak Arithmetic Intensity
Arithmetic Intensity = FLOPS ÷ Memory Bandwidth = 19.5 * 10^12 FLOPS / 2.0 * 10^12 Bytes per sec = 19.5/2 = 9.75 Flops/Byte
Arithemetic Intensity :
To calculate each cell in the output matrix we need to fetch 256 elements from A & 256 Elements from B , and perform 256 Multiply and 256 Additions
To calculate each cell in the output matrix we need to load 8 Tiles each from A & B over several phases, each phase includes 32 Multiply & 32 Addition operations.
Performance Summary
| Approach | Arithmetic Intensity | Memory Efficiency | Category |
|---|---|---|---|
| Naive GEMM | 0.25 FLOP/byte |
2.5% |
Memory-bound |
| Tiled GEMM | 8.0 FLOP/byte |
82% |
Near compute-bound |
Key Improvement: 32× arithmetic intensity gain transforms kernel from memory-bound towards compute-bound operation.